RL - Deterministic policy gradients

• Deterministic policy gradients
  • DPG
    • Note on (discounted) state distribution
  • DDPG
  • TD3

Deterministic policy gradients

Policy gradients 는 기본적으로 stochastic policy $\pi(a|s)$ 를 다룬다. 하지만 대부분의 optimal policy 는 deterministic policy $a=\mu(s)$ 다. 어떤 상황에 정답인 선택지가 딱 정해져 있지, 랜덤하게 두 선택지 중 확률적으로 고르는 것이 optimal 인 경우는 거의 없다는 얘기다. Deterministic policy gradients 계열은 이러한 문제인식으로부터 출발하여 stochastic policy 가 아니라 deterministic policy 를 최적화한다.

DPG

Silver, David, et al. “Deterministic policy gradient algorithms.” ICML. 2014.

• Key idea: 대부분의 task 에서 optimal policy 는 deterministic policy 이므로, 처음부터 deterministic policy 로 학습하자

DPG 는 처음으로 위의 문제를 제기하고 deterministic policy 를 제안한 논문이다. Deterministic policy 를 쓸 경우 expectation 을 취할 때 state 와 action 모두에 대해서 해야 하는 stochastic policy 와는 달리 state 에 대해서만 취하면 되므로 sample efficiency 가 좋아진다.

DPG 에서는 이렇게 deterministic policy 를 취했을 때 이에 대한 deterministic policy gradient 를 구한다:

\[\nabla_\theta J(\mu_\theta) = \mathbb E_{s\sim \rho_\mu}\left[ \nabla_\theta Q^\mu(s,\mu_\theta(s)) \right]\]

여기서 $\rho_\mu$ 는 discounted state distribution 이다. 위 deterministic policy gradient 는 꽤나 직관적인 수식으로, 각 state 에 대해 Q-function 의 기댓값을 최대화하도록 policy update 가 이루어진다. PG theorem 과 같이, state distribution 에 대한 gradient 를 구할 필요가 없다는 것이 DPG theorem 의 핵심이 되며, 증명 과정도 거의 유사하다.

Policy 가 deterministic 이 되면 stochastic policy 에서 자연스럽게 되던 exploration 이 되지 않는 문제가 생긴다. 따라서 DPG 에서는 Q-learning 처럼 노이즈를 주어 exploration 을 수행하는 behavior policy 를 따로 두며, 이를 위한 off-policy DPG 는 다음과 같다:

\[\nabla_\theta J(\mu_\theta) = \mathbb E_{s\sim \rho_b}\left[ \nabla_\theta Q^\mu(s,\mu_\theta(s)) \right]\]

위 식과 비교하면 단지 state distribution 이 behavior policy 로 바뀌었을 뿐이다. 위에서 언급했듯 DPG 가 deterministic 한 특성 때문에 action 에 대해서는 expectation 을 취하지 않는데, 이 덕분에 off-policy DPG 에서도 importance sampling 이 필요 없게 된다.

Note on (discounted) state distribution

이 discounted state distribution 이라는 개념은 (TRPO 에서부터) 상당히 뜬금없이 등장해서 충분한 justification 이 없이 사용되는 경향이 있다. 가장 직관적인 이해로는, undiscounted MDP 세팅에서 모든 state 에서 $1-\gamma$ 의 확률로 terminate 될 수 있다고 가정한다면 $\gamma$-discounted state distribution 이 된다. 사실 이 세팅은 최초 Sutton 의 policy graident paper 에서부터 등장했던 컨셉인데, 사실 실제 환경과는 다소 차이가 있다고도 볼 수 있고 (물론 실제로 terminate 되는 환경일 수도 있지만), 여러가지 이슈가 있어서 지속적으로 관련 논의/연구들이 등장하고 있는 것으로 보인다:

• Reddit: Discounted State Distribution
• Is the Policy Gradient a Gradient?
• Correcting discount-factor mismatch in on-policy PG methods

DDPG

Lillicrap, Timothy P., et al. “Continuous control with deep reinforcement learning.” arXiv preprint arXiv:1509.02971 (2015).

• Key idea: DPG + DQN Critic + Soft target update

앞서 살펴보았듯 DPG 는 off-policy 방법이기 때문에 같은 off-policy 알고리즘인 DQN 의 트릭들을 가져다 사용할 수 있다. DDPG 는 DQN 의 experience replay 와 freeze target network 를 그대로 가져다 적용한다. 그리고 여기에 추가로 target network 를 업데이트 할 때 주기적으로 한번에 업데이트하던 DQN 과는 달리 지속적으로 조금씩 업데이트하는 soft target update 방식을 통해 학습의 안정성을 높였다.

\[L_Q(\phi)=\mathbb E_D \left[ \left( Q_\phi(s,a)-(r+\gamma Q_{\phi^-}(s',\mu_{\theta^-}(s'))) \right)^2 \right]\]

TD3

• Key idea: DDPG + Overestimation bias 해결 + Variance reduction tricks

Fujimoto, Scott, Herke van Hoof, and Dave Meger. “Addressing function approximation error in actor-critic methods.” arXiv preprint arXiv:1802.09477 (2018).

TD3 은 Twin Deplayed DDPG 의 약자로, Q-learning 의 overestimation bias 를 해결하기 위한 twin Q-function 과 variance reduction 을 위한 delayed policy update 를 제안한다.

DQN 에서 발생하는 overestimation bias 를 해결하기 위해 DDQN 에서 double Q-learning 을 도입했었다. TD3 에서는 이러한 bias 가 DDPG 에서도 마찬가지로 발생한다는 것을 보이고, clipped double Q-learning 으로 이를 해결한다.

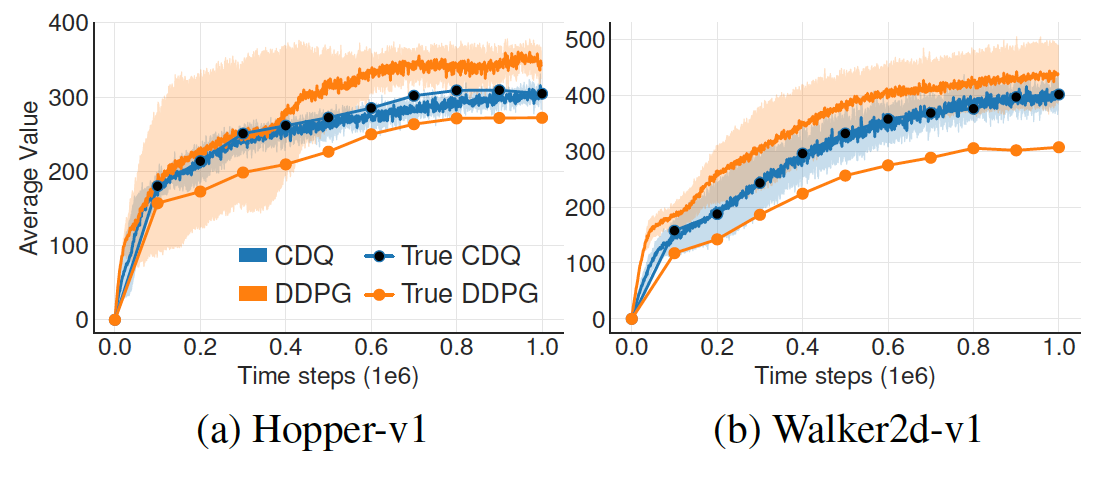CDQ: Clipped Double Q-learning. DDPG 에서도 overestimation bias 가 발생하는 것을 볼 수 있다.

DDQN 에서는 double Q-learning 의 아이디어를 가져와서 이 문제를 해결했지만 actor-critic 세팅에서는 policy 가 천천히 바뀌기 때문에 target network 와 current network 가 크게 다르지 않아서 DPG 에서는 문제를 해결해주지 못한다. TD3 에서는 보다 강력하게 overestimation bias 를 방지하는 Clipped double Q-learning 을 사용한다. 이 방법은 double Q-learning 처럼 Q-function 을 2개 사용하면서 둘 중 낮은 값으로 target y 를 정한다.

\[y=r+\gamma \min_{\text{i=1,2}} Q_{\phi_i^-}(s',\mu(s')+\epsilon) \\ \epsilon \sim \text{clip}(N(0,\sigma), -c, c)\]

위 식에서 policy function $\mu(s)$ 뒤에 noise $\epsilon$ 이 붙어 있는 것을 볼 수 있다. DDPG 의 문제 중 하나는 Q 값이 어쩌다 한번 높게 튀었을 경우, policy 가 그걸 학습하여 exploit 하게 된다는 것이다. 위 noise 는 target policy smoothing regularizer 로, target policy 를 적당히 smoothing 시켜 이러한 문제를 경감시켜 준다.

TD3 의 마지막 트릭은 policy 와 value 의 업데이트 밸런스에 대한 부분이다. 부정확한 value function 을 사용해서 policy 를 업데이트 할 경우 policy 가 망가질 수 있으므로, value function 을 정확하게 학습한 후 policy 를 천천히 업데이트 하자는 아이디어. Value function 을 policy 보다 자주 업데이트하는 delayed policy update 를 통해 밸런스를 맞춘다.