Khanrc
RL - Hierarchical RL
Hierarchical RL
RL 의 agent 는 micro action 으로 움직인다. 앞서 intrinsic motivation 에서 보았던 몬테주마의 복수 게임을 다시 생각해보자.
게임을 해본 적은 없지만, 아마 이 게임에서 액션이라고 하면 좌우 이동과 점프 그리고 사다리가 있다면 내려가는 4개의 상하좌우 키로 구성되어 있을 것이다. 일반적으로 RL 에이전트는 이 액션을 그대로 가져가서, 각 state 에서 상하좌우 중 하나의 액션을 취하고, environment 가 다음 state 를 돌려주면 다시 그에 맞는 액션을 취하는 방식으로 동작하게 된다.
하지만 사람은 이렇게 행동하지 않는다. Intrinsic motivation 에서 설명했듯 몬테주마의 복수 게임은 먼저 열쇠를 먹고 문으로 가야 하는 게임이므로, (충분히 학습된) 사람이 게임을 하면 먼저 1) 열쇠를 먹고 2) 문으로 갈 것이다. 열쇠를 먹으러 갈때 장애물들을 피해서 갈 것이고, 장애물들을 피해 열쇠로 향하기 위해 각 state 마다 적절한 action 을 취할 것이다. 즉 사람은 액션을 정함에 있어서 hierarchy 가 있어서 먼저 상위 액션을 결정하고 상위 액션을 취하기 위해 하위 액션들을 결정하게 된다. Hierarchical RL (HRL) 은 이러한 관점을 따르는 접근법이다.
FuN
Vezhnevets, Alexander Sasha, et al. “Feudal networks for hierarchical reinforcement learning.” Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017.
FuN 에서는 hierarchy 를 주기 위해, micro action 을 수행하는 worker 와, worker 의 goal 을 만들어주는 manager 가 존재한다. Manager 는 상위 액션을 결정하여 worker 에게 goal 을 부여하고, worker 는 이 goal 을 달성하기 위해 움직이게 된다.
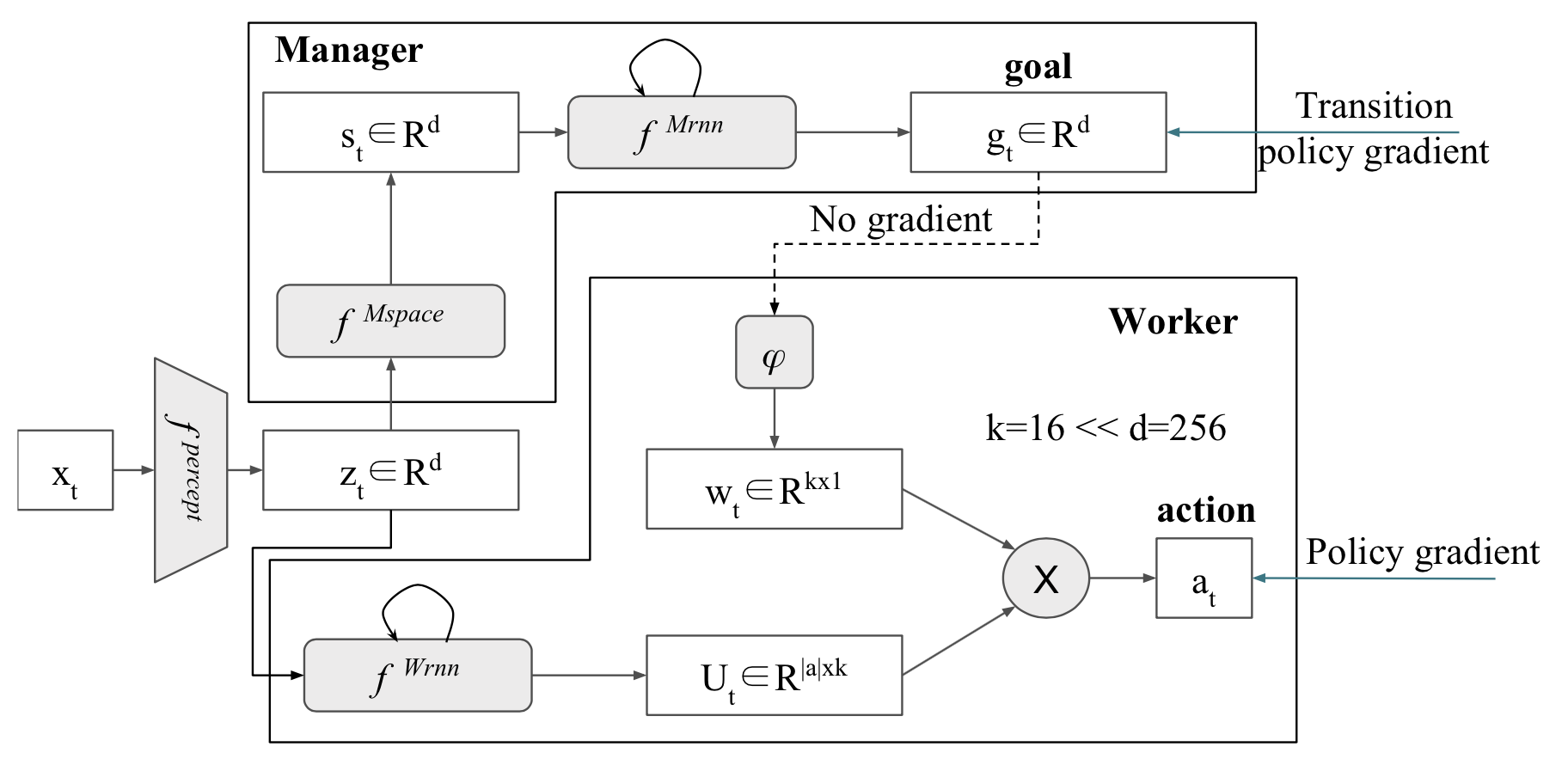 Architecture of FuN algorithm
Architecture of FuN algorithm
Manager 는 이를 위해 state 를 받아서 goal embedding 을 생성하고, worker 는 먼저 action embedding 을 생성한 뒤 goal embedding 과의 연산을 통해서 최종 action 을 결정하게 된다.
이 구조는 사실 fully differentiable 하기 때문에 worker 의 policy gradient 를 manager 로 그대로 흘려넣어서 학습이 가능하다. 하지만 이렇게 되면 manager 가 high-level action 을 잘 생성하도록 학습되리라는 보장이 없기 때문에 의도적으로 중간에 gradient flow 를 끊어준다. $A_t^M$ 이 manager 의 advantage function 이고 $g_t$ 가 goal embedding 이라고 할 때, transition policy gradient $\nabla g_t$ 는:
\[\nabla g_t = A_t^M \nabla_\theta d_{cos}(s_{t+c}-s_t, g_t(\theta)) \\ \text{where} \, A_t^M=R_t-V_t^M(x_t, \theta)\]가 된다. 여기서 $d_{cos}$ 는 cosine similarity 이고, s 는 manager 의 state embedding, x 가 original observation 이다. c step 동안 worker 가 goal 방향으로 잘 이동했는지와 그랬을 때의 advantage value 가 어떻게 되는지를 고려하여 loss 를 계산한다.
위 수식은 policy gradient 수식과 동일한 직관적 해석을 갖는다. Current policy 가 좋은 결과를 얻은 경우 (positive advantage value) 해당 trajectory 대로 움직이도록 action 을 업데이트하고, 좋지 못한 결과를 얻었을 경우 (negative advatnage value) 해당 trajectory 와 다르게 행동하도록 action 을 업데이트한다. 여기서 manager 의 action 이 곧 goal $g_t$ 다.
Worker 는 manager 가 생성한 goal embedding 방향으로 잘 이동하였는지에 따라 intrinsic reward 를 받는다:
\[r_t^I = \frac 1c \sum^C_{i=1} d_{cos}(s_t-s_{t-i}, g_{t-i})\]최종적으로 worker 가 받는 reward $R_t^W$ 는 intrinsic reward $R_t^I$ 와 environment reward $R_t$ 를 섞는다.
\[R_t^W = R_t + \alpha R_t^I\]One step more: FuN on the Montezuma’s revenge
FuN 논문에서는 몬테주마의 복수 게임에서 일정 수준 이상의 학습이 가능하며, 이 때 manager 가 semantic meaningful goal 을 생성한다는 것을 보여준다.
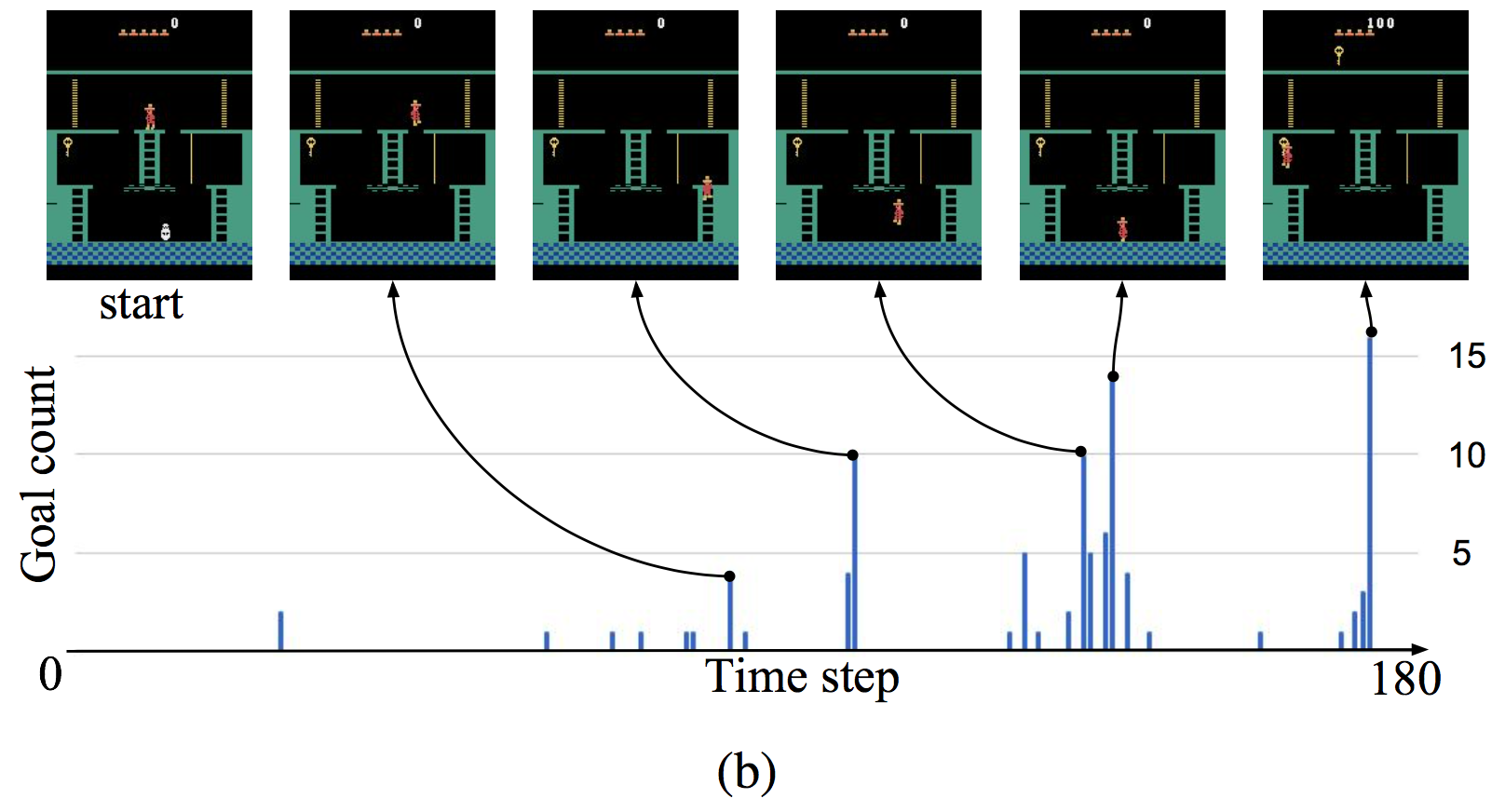
위 그래프가 총 180 timestep 이라고 하면, 이 trajectory 에는 180개의 state 와 goal 이 있을 것이다. 이 때 goal 에서 가장 가까운 future state 를 찾아서 goal count 를 1씩 증가시킨다. 즉, 어떤 state 의 goal count 가 10이라면 해당 state 와 가장 가까운 past goal 이 10개가 있다는 것이고, manager 가 해당 state 를 goal 로 10번 생성했다는 것이다. 결국 이 그래프가 높은 지점이 FuN 프레임웤이 생각하는 sub-goal 에 해당한다.
이렇듯 FuN 은 몬테주마의 복수에서 유의미한 성과를 거뒀다. 그런데 잘 생각해보면 HRL 은 몬테주마의 복수 같은 sparse reward problem 과 관련이 없다. Intrinsic motivation 섹션에서 살펴보았듯, sparse reward problem 에서는 초기 랜덤 폴리시로 reward 를 받는 것이 불가능하기 때문에 학습이 안 되고, 이 문제를 해결하기 위해 보다 좋은 exploration 을 하자는 것이 intrinsic motivation 이었다. FuN 에서 이러한 exploration 방법을 도입한 것도 아닌데 어떻게 이 문제를 해결할 수 있었을까?
FuN works like HER
FuN 은 초기 exploration 단계에서 HER (Hindsight Experience Replay) 와 유사하게 작동한다. Sparse reward problem 특성상 초기 exploration 단계에서 environment reward 는 받을 수 없지만, 대신 manager 가 생성하는 goal 에 의해 worker 는 intrinsic reward 를 받게 된다. 이 intrinsic reward 는 uncertainty 를 기반으로 하는 intrinsic motivation 방법과 달리 좋은 exploration 을 하게 해 주지는 않지만, 어쨌든 앞으로 나아가게 해 준다.
직관적으로 비유하자면, 아이를 가르칠 때 뭘 하든 비난만 하는 케이스와 뭘 하든 칭찬을 해주는 경우를 비교해보자. 만약 무얼 하든 비난만 한다면 아이는 그저 아무것도 하지 않는 사람으로 성장할 것이다. 하지만 설령 옳은 방향이 아닐지라도 칭찬을 계속 해 주면 아이는 그 방향으로 나아갈 것이고, 어떻든 무언가를 익힐 수 있을 것이다. 그리고 처음으로 돌아와서 이 과정을 반복하면 다양한 여러가지 기술을 익힐 수 있을 것이고, 그러다 보면 원래 목표했던 goal 에 도달할 수 있을 것이다.
이와 같이, HER 은 실제로 목표한 goal 에 도달하지 못했더라도 reward 를 부여하여 어떻든 무언가를 배우고 앞으로 나아가게 하여 결국에는 goal 에 도달할 수 있도록 하는 방법이다. FuN 또한 초기에 manager 가 랜덤한 goal 을 생성하겠지만, 어떻든 worker 는 그 goal 로 향하도록 학습이 될 것이다. 계속 environment reward 를 받지 못하더라도 manager 가 헤매는 동안 worker 는 manager 가 지정한 goal 로 향하는 방법을 배울 것이고, 결국에는 부족한 manager 이더라도 똑똑한 worker 에 힘입어 goal 에 도달하여 environment reward 를 받아내고 학습이 가능해진다.
추후 HER 내용이 포함된 Transfer and Multitask RL 파트 포스팅 시 위 내용 업데이트 예정.
HIRO
Nachum, Ofir, et al. “Data-efficient hierarchical reinforcement learning.” Advances in Neural Information Processing Systems. 2018.
- Key idea: FuN + TD3 + off-policy correction
HIRO 는 FuN 의 직관을 유사하게 가져간다. FuN 과 같이 2-level hierarchy policy 를 사용하지만 용어가 조금 달라지는데, manager 를 high-level policy, worker 를 low-level policy 라 부른다. Sample efficiency 를 위해 off-policy algorithm 인 TD3 을 사용하는데, HRL 에서 off-policy 를 쓸 때 생기는 문제를 off-policy correction method 를 통해 해결한다.
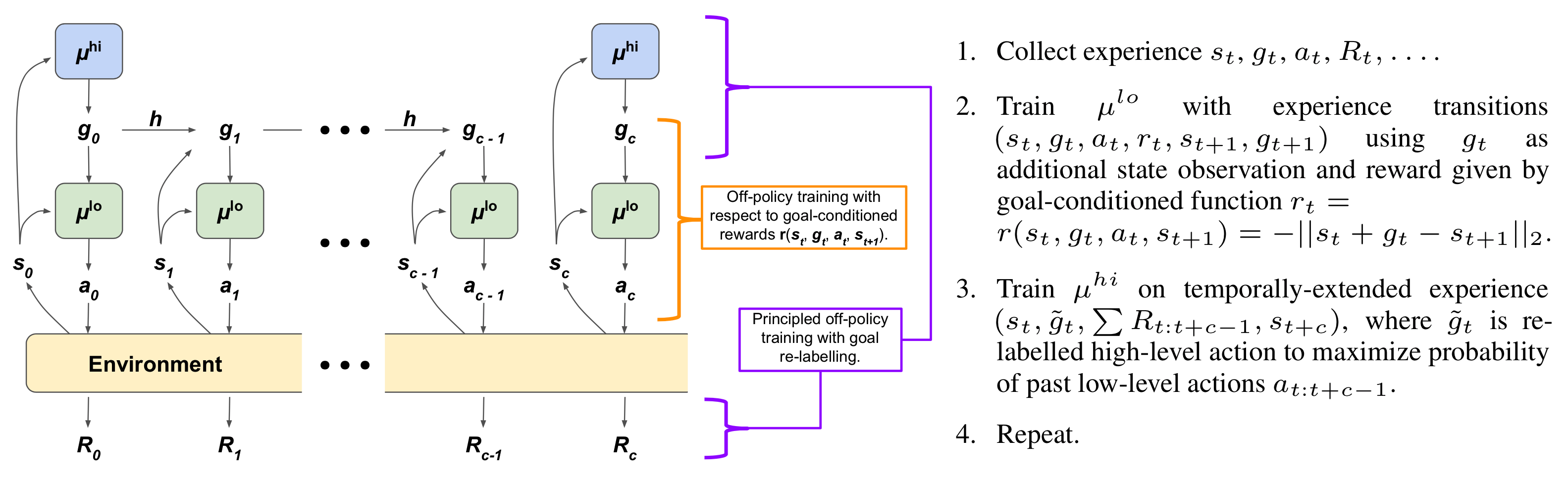 Architecture and algorithm of HIRO
Architecture and algorithm of HIRO
HIRO 의 구조와 알고리즘은 위 그림 한장에 잘 설명되어 있다. FuN 과의 차이를 살펴보면, 1) goal 을 매 step 새로 생성하지 않고 한번 생성한 goal 을 c step 동안 유지한다. transition function h 는 단지 state 가 바뀔 때 그에 맞게 goal 을 업데이트 해주는 역할을 할 뿐이다. 2) low-level policy 가 액션을 할 때 직접적으로 goal 을 고려하지는 않는다. reward 를 계산할 때만 고려한다. 3) FuN 에서는 goal 은 cosine similarity 를 통해 direction 만 가이드했으나, HIRO 에서는 그냥 L2-distance 로 계산하기 때문에 정확한 goal position 을 가이드한다.
구체적으로 각 policy 의 reward 를 어떻게 계산하는지 살펴보자. High-level policy 는 c step 마다 goal state 를 생성하고, 이것이 곧 high-level policy 의 action 이다. c step 동안 얻은 environment reward 를 모아서 high-level transition $(s_t, \tilde g_t, \sum R_{t:t+c-1}, s_{t+c})$ 를 얻을 수 있다. FuN 과 같이 high-level policy 의 action 이 곧 goal 이므로, 위 transition 은 (s, a, r, s’) 에 해당한다.
Low-level policy 를 위한 intrinsic reward 는 goal state 와의 distance 로 계산된다. Goal state 를 현재 state $s_t$ 에서의 relative position 으로 다루기 때문에 state 가 바뀌면 goal state 도 따라 바뀌게 되고, 이를 위해 goal transition function h 를 사용한다:
\[h(s_t,g_t,s_{t+1})=s_t+g_t-s_{t+1}\]이제 각 타임스텝의 goal state 를 알았으니 이를 이용하여 distance 를 계산하여 reward 로 사용한다:
\[r(s_t, g_t, a_t, s_{t+1})= - \lVert s_t + g_t - s_{t+1} \rVert\]이제 각 policy 의 reward 를 계산하였으니 TD3 으로 학습을 하면 되는데, 위 high-level transition 을 잘 보면 goal 에 tilde 가 붙어있는 것을 확인할 수 있다. TD3 과 다르게 HIRO 에서는 low-level policy 가 존재하므로 같은 (s, g) 라 하더라도 다른 low-level policy 를 갖는다면 그 trajectory 가 달라진다. 따라서 학습할 때 current low-level policy 에 맞게 goal state 를 조정해주는 off-policy correction 작업이 필요하다. Current low-level policy 를 따를 때 해당 trajectory 가 나오도록 goal state 를 조정한다:
\[\arg\min_{g_t} \sum^{t+c-1}_{i=t} \lVert a_i - \mu^{lo}(s_i, \tilde g_i) \rVert^2_2\]실제로 구현할 때에는 $\tilde g_t$ 를 $s_{t+c}-s_t$ 근처에서 적당히 몇 개 샘플링하여 minimum 을 근사한다.
STRAW
Vezhnevets, Alexander, et al. “Strategic attentive writer for learning macro-actions.” Advances in neural information processing systems. 2016.
STRAW 는 FuN 이나 HIRO 와는 다소 다른 접근방법을 취한다. 처음 예제로 돌아와서, 몬테주마의 복수 게임을 푼다고 해 보자. 앞서 설명했듯 사람이라면 1) 열쇠를 먹고 2) 문으로 가자는 high-level goal 을 설정할 것이고, 이 goal 을 달성하기 위해 micro action 을 취할 것이다. 그런데 이 부분을 조금 더 구체적으로 생각해보면, 사람은 goal 을 달성하기 위해 plan 을 짠다. 매 순간순간 판단해서 action 을 취하는 것이 아니라, 처음에 상황을 보고 action plan 을 짠 다음에 순간순간의 상태 변화에 따라 주기적으로 plan 을 수정한다. 만약 goal 에 도달했다면 그 시점에 다음 goal 을 향한 새로운 plan 을 짤 것이다.
STRAW 는 이와 같은 action plan 컨셉을 도입한다. State 로부터 현재 action 만 취하는 것이 아니라, 앞으로에 대한 action plan 을 짜고, 언제쯤 plan 을 업데이트 할지를 가리키는 commitment plan 까지 결정한다.
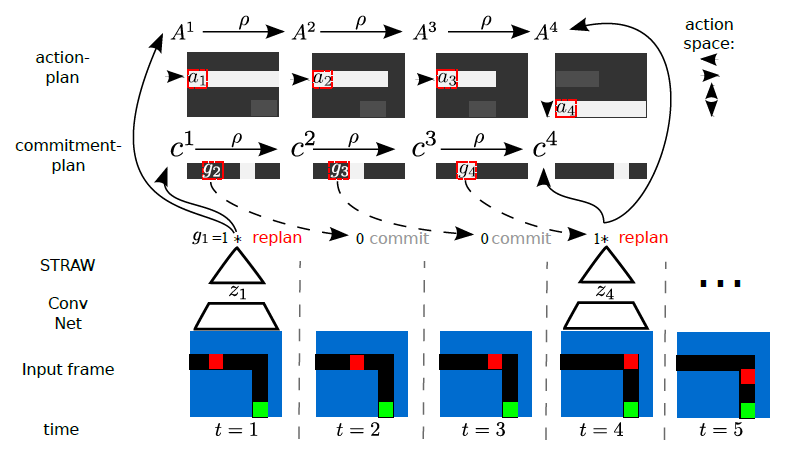 Overview of STRAW algorithm
Overview of STRAW algorithm
이 그림에서 replan 이라는 것이 plan 업데이트에 해당한다. 이 replan 은 현재의 state embedding 을 기반으로 기존의 action plan 을 업데이트하는데, 이 때 경우에 따라 action plan 의 크기가 한번에 고려하기에는 너무 클 수 있으므로 중요한 부분에 attention 하는 기법을 사용하며 이를 attentive planning 이라고 한다:
- action plan $A^t$ 로부터 state embedding $z_t$ 를 고려하여 attention 을 통해 action patch 를 뽑아낸다 (read).
- 여기서 다시 $z_t$ 를 고려하여 action patch 를 업데이트한다.
- 업데이트한 action patch 를 다시 기존 action plan 에 반영한다 (write).
이를 그림으로 나타내면 다음과 같다:
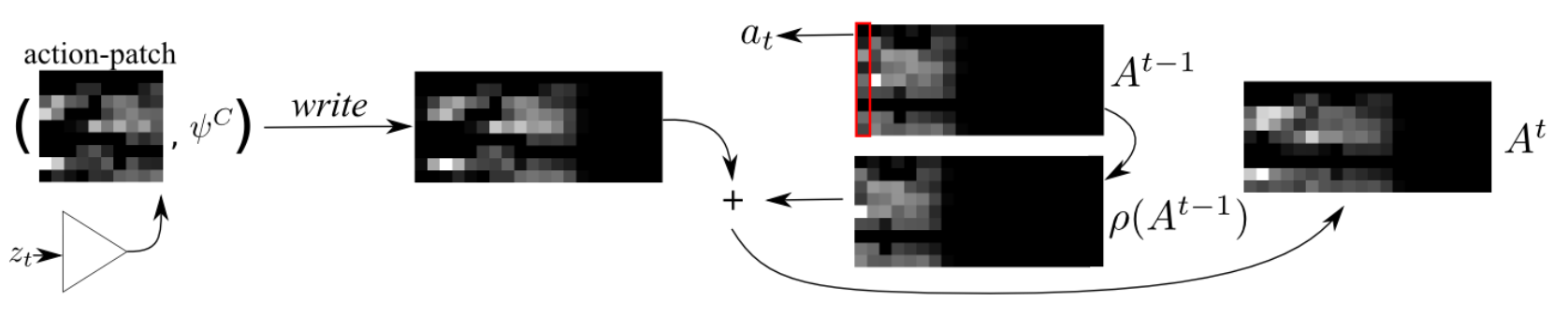 Attentive planning
Attentive planning
이 replanning 이 너무 자주 일어나면 안 되므로 replan signal $c^t$ 자체를 loss 로 사용하여 replanning 에 핸디캡을 준다. 여기에 학습 알고리즘으로는 A3C 를 사용했다:
\[\begin{align} L=\sum^T_{t=1} \left( L^{out}(A^t)+g_t\cdot \alpha KL(Q(z_t|\xi_t)|P(z_t)) + \lambda c_1^t \right) \\ \nabla L^{out}=\nabla_\theta \log \pi_\theta(a_t|x_t)A_\theta(x_t)+\beta \nabla_\theta H(\pi_\theta) \end{align}\]중간에 설명하지 않은 텀이 하나가 나온다. 이 $Q(z_t|\xi_t)$ 는 action plan 에 추가적으로 noise 를 준 STRAW-explorer (STRAWe) 버전이다. 여기에 KL divergence 로 페널티를 주어 noise 가 너무 prior $P(z_t)$ 에서 벗어나지 않도록 한 것이다.