Khanrc

RL - Intrinsic Motivation

Intrinsic Motivation

RL 이 맞닥뜨리는 주요한 챌린지 중 하나는 sparse reward 다. RL 은 처음에 랜덤 폴리시로 시작한다. 이 말은 곧 랜덤 폴리시로 reward 를 받을 수 있어야 학습이 가능하다는 의미다. 때문에 sparse reward 인 경우, 랜덤 폴리시로 reward 를 받을 수가 없어 학습이 전혀 되지 않는다.

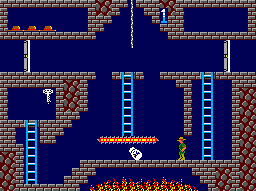montezuma Sparse reward problem 으로 유명한 몬테주마의 복수 게임

몬테주마의 복수 게임은 몬스터를 피해 열쇠를 먹고 문으로 가야 하는 게임이다. 몬스터를 피해서 열쇠를 먹고 다시 몬스터를 피해 문까지 가야 리워드를 받을 수 있는 sparse reward 환경인 것이다. 이러한 환경에서 랜덤 액션 폴리시로 reward 를 받기란 불가능에 가깝기 때문에, 지금까지 소개된 기존의 알고리즘들은 거의 학습이 불가능했다.

이러한 문제를 해결하기 위해 제안된 여러가지 방법이 있다. 그 중 intrinsic motivation 은 exploration 을 어떻게 더 잘할 수 있을까에 대한 방법이다. 지금까지 소개된 exploration 방법들은 대부분 random exploration 에 의존한다. 하지만 사람의 경우 exploration 을 할 때에도 완전 랜덤이 아니라 여러가지 기준이 있다. 그리고 그 기준 중 중요한 하나는 “이전에 해보지 않은 것” 이다. 이전에 많이 가본 state 보다 별로 가보지 않은 state 를 exploration 하는 것이 좋을 것이다. 이와 같이 이전에 해보지 않은 것에 대한 동기부여를 intrinsic motivation 이라고 하며, curiosity-based RL 이라고도 불린다.

CTS-based Pseudocounts

Bellemare, Marc, et al. “Unifying count-based exploration and intrinsic motivation.” Advances in Neural Information Processing Systems. 2016.

Pseudocounts 는 이전까지 거의 학습을 하지 못하던 몬테주마의 복수 게임에서 처음으로 성과를 보인 논문이다. 앞서 설명했듯 이러한 sparse reward 환경에서 이전에 가보지 못한 state 에 동기부여를 주는 방식으로 문제를 해결한다. Count-based 라는 것은 각 state 에 카운팅을 해서 얼마나 가봤는지를 체크하는 방법이다.

\[V(s)=\max_a \left[ r + \gamma \mathbb E[V(s)] + \beta N(s,a)^{-1/2} \right]\]

위 수식은 MBIB-EB (2008) 에서 제안된 수식으로, state-action pair (s,a) 에 대해 counting 을 하고, 이를 기반으로 uncertainty 를 계산하여 intrinsic reward 로 사용한다. 하지만 이 방법은 정말로 모든 state-action pair 를 카운팅하므로 state(-action) space 가 커지면 적용이 불가능하며, 설령 할 수 있다 하더라도 state 가 1픽셀의 RGB 값이 1만 달라져도 다른 state 가 되므로 이 state 가 얼마나 새로운지를 나타내는 수치가 될 수 없다.

이 논문의 핵심 contribution 은 이러한 문제를 해결하기 위해 count-based uncertainty approximator 를 통해 approximated count, 즉 pseudo-count 를 계산한 것이다. 이를 계산하기 위해 density model $\rho(s)$ 를 모델링하여 사용하는데, 이 때 density model 로 사용하는 것이 바로 Context Tree Switching (CTS) 이라서 이름에 CTS-based 가 붙었다.

이 density model $\rho(s)$ 를 사용해서 아래 두 식을 정의할 수 있다:

\[\rho_n(s)=\rho(s; s_{1:n}) \\ \rho'_n(s)=\rho(s; s_{1:n}s)\]

첫번째 식은 sequence $s_1, s_2, …, s_n$ 을 보았을 때 다음에 $s$ 가 등장할 확률이고, 두번째 식은 sequence $s_1, s_2, …, s_n, s$ 를 보았을 때 다음에 $s$ 가 또 등장할 확률이다. 그러면 이 두 식을 활용해서 pseudo-count $\hat N$ 을 구할 수 있다:

\[\hat N_n(s)=\frac{\rho_n(s)(1-\rho'_n(s))}{\rho'_n(s)-\rho_n(s)}\]

이 pseudo-count 는 곧 intrinsic reward 가 된다:

\[R^+_n(s,a)=\beta (\hat N_n(s) + 0.01)^{-1/2}\]

Pseudocount 는 이러한 방법으로 몬테주마의 복수 게임에서 처음으로 학습에 성공한다.

cts-montezuma-results Results on Montezuma’s revenge with DQN w/ and w/o pseudocount bonus

몬테주마의 복수 게임은 각 스테이지가 방으로 구성되어 있어 방에서 탈출해서 다른 방으로 이동해야 한다. Pseudocount 를 사용하지 않은 No bonus 세팅에서는 거의 학습이 안 되었지만, with bonus 세팅에서는 절반 이상 클리어한 것을 확인할 수 있다.

ICM

Pathak, Deepak, et al. “Curiosity-driven exploration by self-supervised prediction.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. 2017.

Intrinsic Curiosity Module (ICM) 에서는 이러한 uncertainty 의 측정을 네트워크의 예측력 기반으로 바꾼다. 현재 state 와 action 을 기반으로 다음 state 를 예측하는데, 이 예측 정도가 얼마나 정확한지에 따라 uncertainty 를 매겨 intrinsic reward $r^i$ 를 생성한다. 직관적으로, 많이 가본 state 라면 예측을 잘 할 것이므로 uncertainty 가 낮을 것이고 그렇지 않은 state 라면 예측을 잘 못할 것이므로 높은 uncertainty 가 나올 것이다.

\[\hat\phi(s')=f(\phi(s), a) \\ r^i=\frac{\eta}{2} \lVert \hat\phi(s') - \phi(s') \rVert\]

feature 를 추출하는 embedding network $\phi$ 와 현재 state 와 action 을 기반으로 다음 state 를 예측하는 forward model $f$ 를 학습하여 사용한다. 이름 그림으로 표현하면:

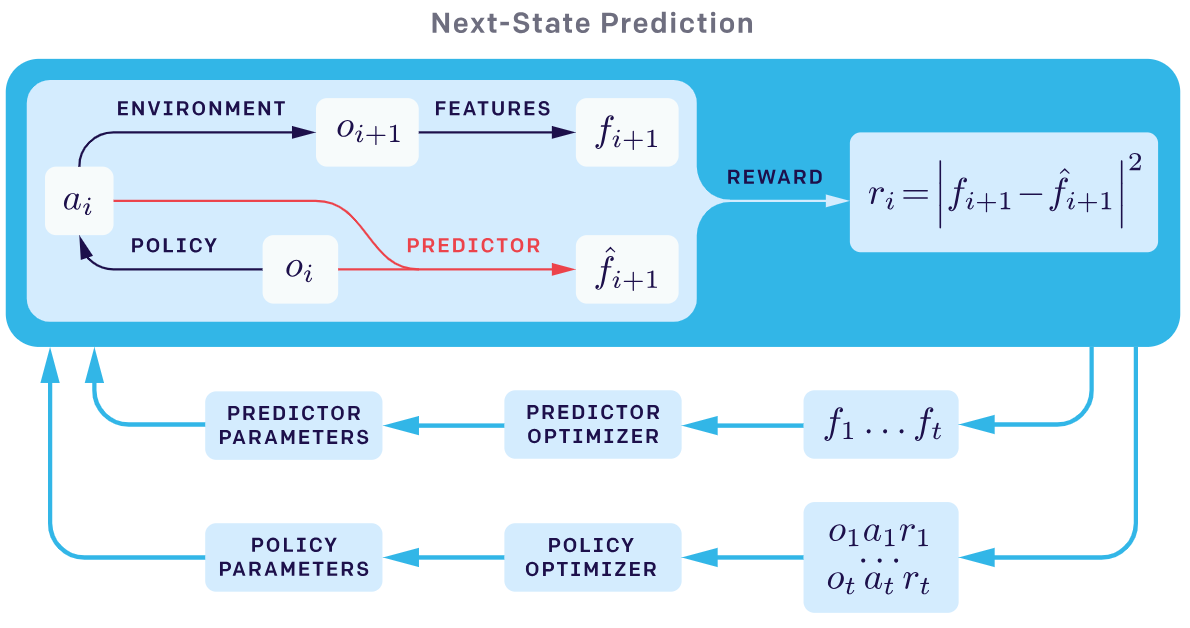icm-architecture Adapted from OpenAI blog post: RL with Prediction-Based Rewards

위 그림은 용어가 조금 다른데, predictor 가 forward model 이고 observation $o$ 가 state $s$ 에 해당한다.

여기서 feature 를 추출하는 embedding network 를 inverse model 이라고 부르며 현재 state 와 다음 state 를 통해 현재 action 을 잘 예측하도록 self-supervised learning 을 수행한다.

이와 같이, 해결하고자 하는 문제의 정답 label 이 있는 것은 아니지만 embedding (feature) network 학습을 목적으로 주어진 데이터 내에서 target 을 정해 학습하는 방식을 self-supervised learning 이라 부른다.

RND

Burda, Yuri, et al. “Exploration by random network distillation.” arXiv preprint arXiv:1810.12894 (2018).

Random Network Distaillation (RND) 은 ICM 의 직관을 그대로 가져오면서 ICM 이 갖는 문제점을 해결한다. Stochastic 한 environment 라면, 동일한 현재 state 와 action 이라도 다음 state 가 stochastic 하게 변할 수 있다. ICM 은 현재 state 와 action 으로 다음 state 를 얼마나 잘 예측하는지로 uncertainty 를 측정하기 때문에, 다음 state 가 충분히 많이 방문하여 익숙한 상황이라도 stochastic 한 state 에서는 높은 uncertainty 를 갖게 된다.

RND 는 다음 state 를 예측하는 대신, state 로부터 랜덤한 feature 를 추출하는 랜덤 네트워크를 두고 그 값을 target 으로 predictor 를 학습시켜 environment 의 stochasticity 에 영향받지 않도록 구성하였다. 랜덤 네트워크는 key idea 에서 이야기했던 것처럼 state 에 대해 deterministic 하여 같은 state 라면 같은 feature 를 추출하며, 동시에 유사한 state 라면 유사한 feature 를 추출하기 때문에 feature network 로 사용할 수 있다.

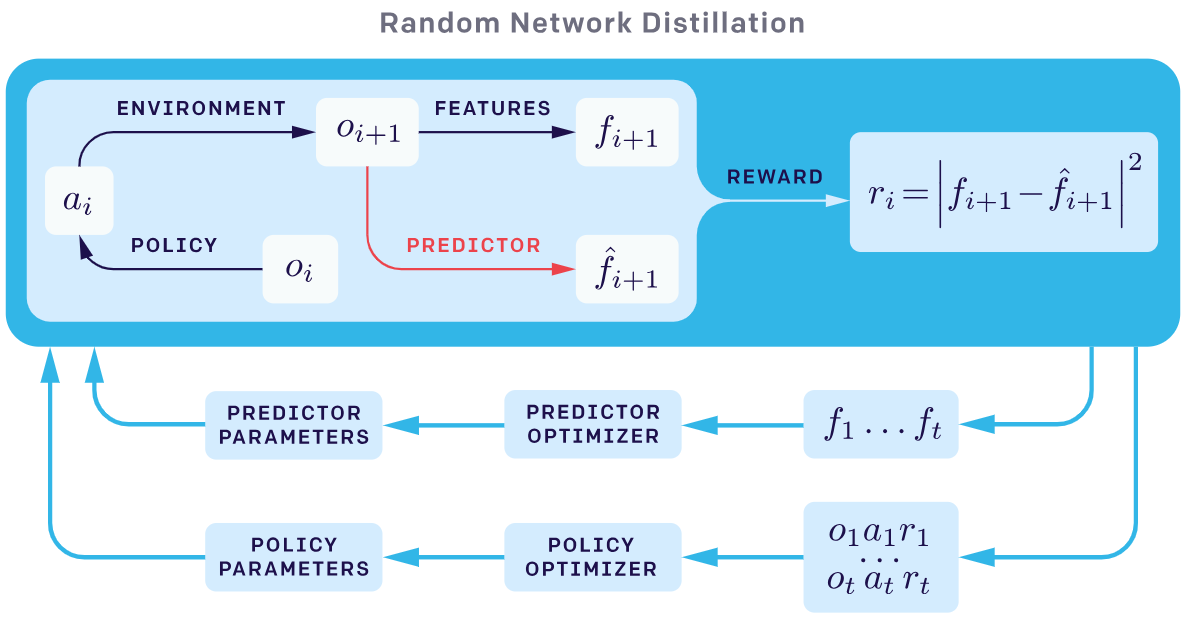rnd-architecture Adapted from OpenAI blog post: RL with Prediction-Based Rewards

RND 에서는 이러한 방법을 통해 처음으로 몬테주마의 복수 게임에서 사람의 성능을 뛰어넘었다.

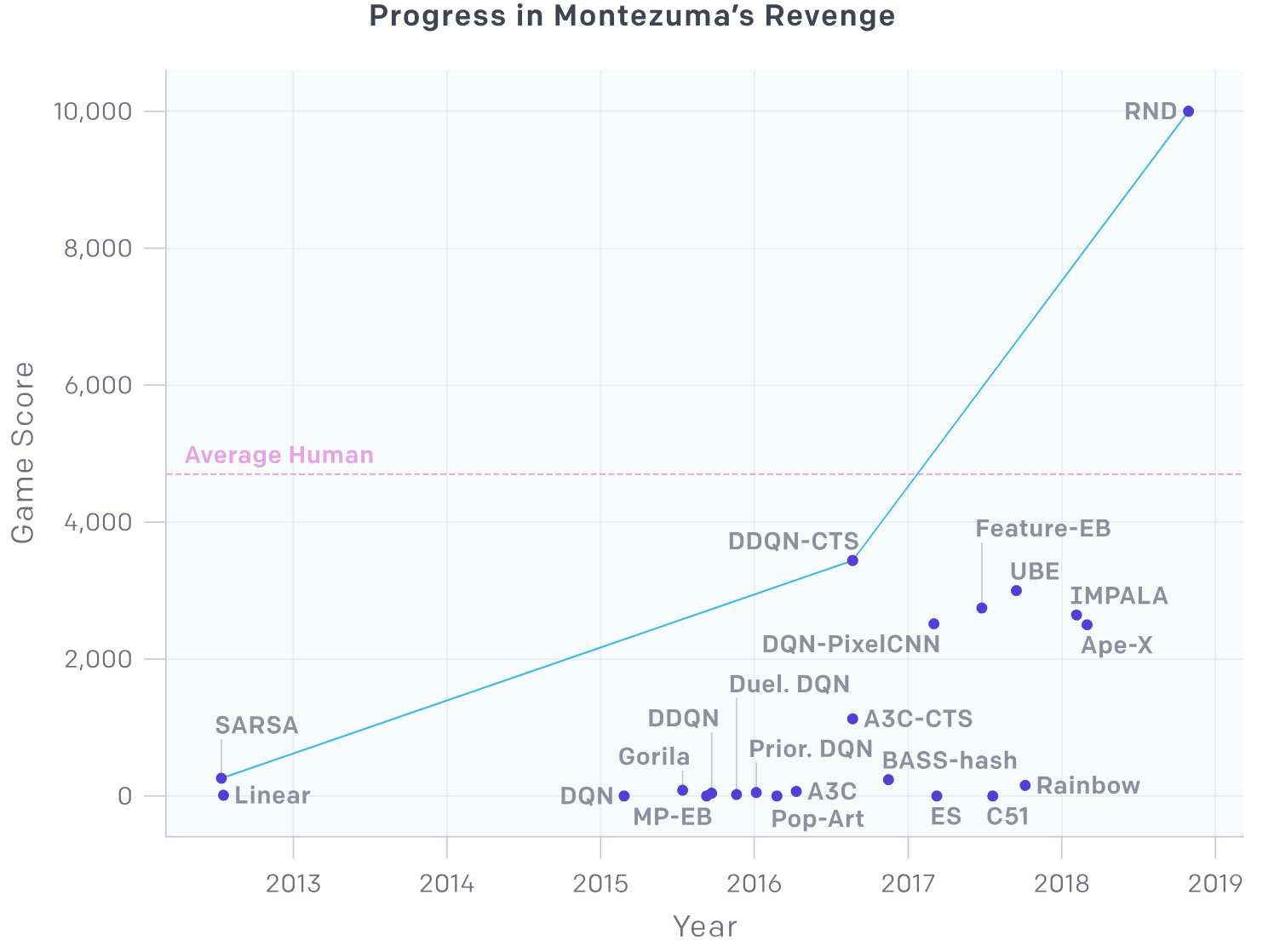rnd-score Adapted from OpenAI blog post: RL with Prediction-Based Rewards