Khanrc

RL - Policy gradients

Policy gradients

추천 레퍼런스:

NPG, TRPO, PPO:

Policy Gradient Theorem

Sutton, Richard S., et al. “Policy gradient methods for reinforcement learning with function approximation.” Advances in neural information processing systems 12 (1999).

Reward function $J(\theta)$ 는 다음과 같이 정의할 수 있다:

\[J(\theta) = \sum_{s \in \mathcal{S}} d^\pi(s) V^\pi(s) = \sum_{s \in \mathcal{S}} d^\pi(s) \sum_{a \in \mathcal{A}} \pi_\theta(a \vert s) Q^\pi(s, a)\]

where \(d^\pi(s)\) is the stationary distribution of Markov chain for \(\pi_\theta\) (on-policy state distribution).

이제 으레 하듯이 이 reward function 를 gradient ascent 로 maximize 하고 싶은데, 여기서 문제는 state distribution \(d^\pi(s)\) 의 gradient 를 계산하기가 어렵다는 것이다. Policy graident theorem 은 바로 이 문제를 해결하는 theorem 으로, 다음과 같은 policy gradient 수식을 얻을 수 있다:

\[\nabla_\theta J(\pi_\theta)=\mathbb E_{\tau\sim \pi_\theta} \left[ \sum^T_{t=0} Q^{\pi_\theta} (s_t, a_t) \nabla_\theta \ln \pi_\theta (a_t|s_t) \right]\]

여기서 여러가지 변주를 줄 수 있는데, GAE 논문에 잘 정리되어 있다.

pg-gae

여기서 1, 2번이 REINFORCE 에 해당하고, 3번이 REINFORCE with baseline, 4, 5, 6번이 Actor-Critic 에 해당한다.

REINFORCE

Williams, Ronald J. “Simple statistical gradient-following algorithms for connectionist reinforcement learning.” Machine learning 8.3-4 (1992): 229-256.

REINFORCE 는 위 피규어에서 1, 2, 3 에 해당하는 방법론이다. 이 세가지 수식이 전부 같은 expectation 값을 갖는데, 앞쪽 수식일수록 variance 가 크다. Q-learning 계열도 마찬가지지만 PG 계열에서도 expectation 을 sampling 으로 대체하게 되는데, 여기서 발생하는 variance 를 잡는 것이 주요한 챌린지가 되며, REINFORCE 에서도 variance 를 줄이기 위한 노력들을 엿볼 수 있다.

\[\nabla_\theta J(\pi_\theta)=\mathbb E_{\tau\sim \pi_\theta} \left[ \sum^T_{t=0} (G_t-b(s_t)) \nabla_\theta \log \pi_\theta (a_t|s_t) \right]\]

여기서 $G_t$ 는 timestep t 에서의 expected return, $b(s_t)$ 는 baseline 에 해당한다. REINFORCE 는 return G 를 알아야 하기 때문에 하나의 에피소드가 끝나야만 학습을 수행할 수 있다.

Actor-Critic

Actor-critic 에서는 return G 를 Q-network 으로 approximate 하고, bootstrapping 을 통한 학습을 함으로써 에피소드가 끝나지 않아도 학습이 가능해진다. 이 Q-network 은 actor (policy) 의 행동을 평가하는 역할을 하기 때문에 critic 이라고 부른다.

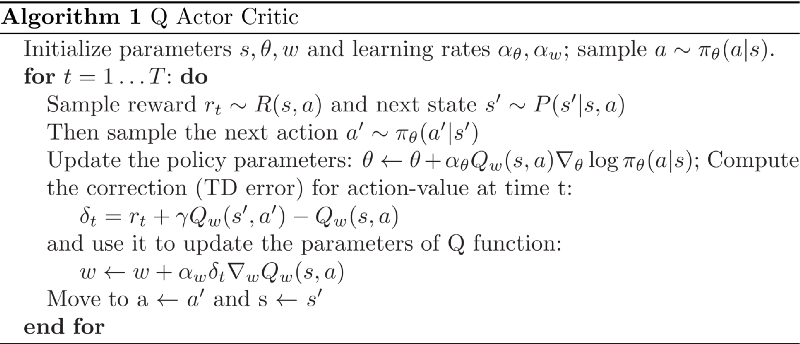
pg-ac-alg

Actor-critic 은 이러한 Q actor-critic 외에도 여러 종류가 있다:

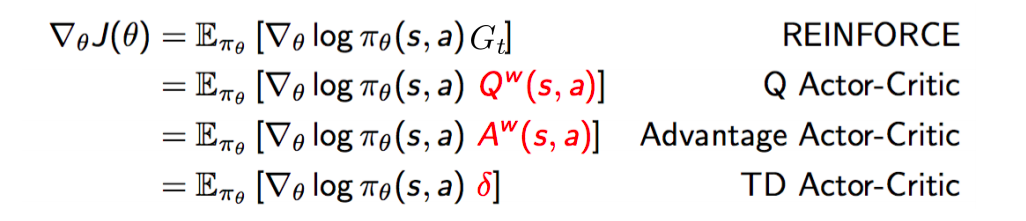pg-actor-critic Image taken from CMU CS10703 lecture slides

Critic 으로 advantage function A(s,a) 를 사용하는 advantage actor-critic 이 바로 A2C 다. 여기서 여러개의 actor 를 두고 업데이트를 asynchronous 하게 수행하는 A3C 로 발전한다.

Off-policy Actor-Critic

Degris, Thomas, Martha White, and Richard S. Sutton. “Off-policy actor-critic.” arXiv preprint arXiv:1205.4839 (2012).

PG 계열 알고리즘들은 기본적으로 on-policy 다. Expectation 항을 보면 trajectory $\tau$ 가 current policy $\pi_\theta$ 에서 sampling 되기 때문에 과거의 trajectory 를 사용할 수 없다. Off-policy actor-critic 에서는 importance sampling 을 이용하여 off-policy policy gradient 를 유도하고, 이것이 근사식임에도 local optima 로 수렴한다는 것을 증명한다.

\[\nabla_\theta J_b(\pi_\theta)=\mathbb E_{\tau\sim \pi_b} \left[ \frac{\pi_\theta(a|s)}{b(a|s)} Q^{\pi_\theta}(s,a) \nabla_\theta \log \pi_\theta(a|s) \right]\]

A3C

Mnih, Volodymyr, et al. “Asynchronous methods for deep reinforcement learning.” International conference on machine learning. 2016.

A3C 는 Asynchronous Advantage Actor-Critic 로, Advantage Actor-Critic (A2C) 의 asynchronous parallel 버전이다. 여러 쓰레드에 각각 actor 를 두고 동시에 simulation 을 하고, 각 액터는 gradient 를 계산해서 누적하여 갖고 있다가 주기적으로 policy network 와 value network 를 업데이트 해 준다.

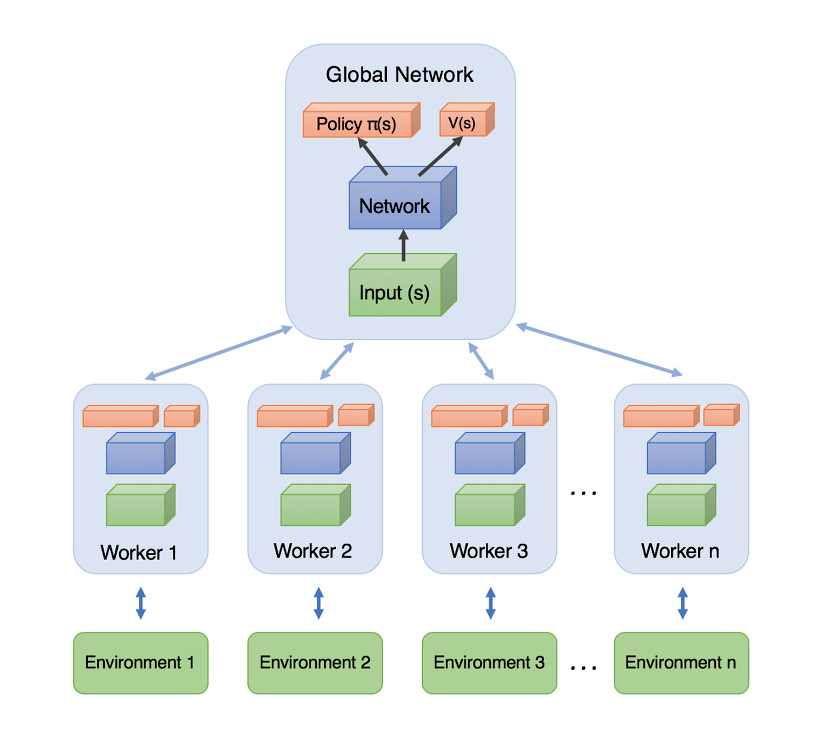
pg-a3c

재미있는 점은 이 때 동기화 과정이 없다는 것이다. 원래대로라면 Global network 를 갖고 있는 마스터 노드에서 각 그라디언트를 취합하여 네트워크를 업데이트하고, 다시 이 네트워크를 각 액터 쓰레드에 뿌려서 parallel simulation 을 수행해야 한다. 하지만 이러한 synchronous 방식은 동기화 과정에서의 오버헤드가 크기 때문에 이를 최소화하기 위해 asynchronous 방식을 사용하는데, 각 액터에서 그라디언트를 서버로 전송하면 서버는 여러 액터들의 시뮬레이션 종료까지 기다려서 동기화를 하는 대신 바로 네트워크를 업데이트하고 이 네트워크를 액터로 다시 내려보낸다. 즉, 액터-마스터 간 동기화 과정은 있지만 액터끼리는 동기화가 되지 않는 것이다.

따라서 각 액터들은 서로다른 네트워크를 사용하여 시뮬레이션을 진행하게 되며, global network 는 과거의 파라메터가 만든 그라디언트로 업데이트가 진행되게 된다. 예를 들어 설명해보자. 4개의 워커가 있을 때, global network $\theta_1$ 로 처음 시뮬레이션을 시작한다고 하고, 시뮬레이션은 워커 순서대로 종료되었다고 가정하자. 그러면 이 때 워커1 의 시뮬레이션이 끝나고 그라디언트 업데이트를 하게 되면 global network 가 $\theta_2$ 로 업데이트되는데, 이후 워커2 의 시뮬레이션이 종료되면 $\theta_1$ 에 의해 생성된 그라디언트들이 $\theta_2$ 를 업데이트 하게 된다! 이는 워커4 로 가면 더 심해져서 $\theta_1$ 에 의해 생성된 그라디언트로 $\theta_4$ 를 업데이트 하게 될 것이다.

이러한 방식의 네트워크 트레이닝을 asynchronous training 이라고 하며, 과거 노드 간 커뮤니케이션 코스트가 심하던 시절 분산 트레이닝에도 활용되어 성과를 보였다. RL 에서도 예전부터 이러한 방식의 optimization 이 연구되었으며 잘 작동한다고 알려져 있다.

이 논문에서는 A3C 만 제안한 것은 아니고 asynchronous DQN 등 여러 알고리즘에 대해서 적용해 보았으나 A3C 가 가장 성능이 좋았다. A3C 에는 parallel training 외에도 몇 가지 트릭이 더 쓰였는데, 1) entropy regularization 을 통해 exploration 을 강화하고 2) 각 워커마다 exploration policy 를 다르게 주어 보다 다양한 경험을 수집하고 3) multi-step learning (n-step TD) 을 통해 variance 를 잡았고 4) 네트워크에 LSTM 을 붙여 sequential modeling 까지 잡았다.

One step more: A2C is better than A3C

OpenAI blog post 에 따르면, A3C 에서 asynchronous 는 성능 향상에 별다른 도움이 되지 않았으며, 오히려 (synchronous) A2C 가 성능이 더 좋다고 한다. 단지 빠른 학습을 위한 implementation detail 으로 보이고, 사실 지금 시대에서는 그다지 쓰일 곳이 많지 않을 방법론이다.

GAE

Schulman, John, et al. “High-dimensional continuous control using generalized advantage estimation.” arXiv preprint arXiv:1506.02438 (2015).

앞서 언급했듯 RL 의 주요한 이슈중 하나는 sampling 으로부터 생기는 variance 를 어떻게 잡느냐다. 이 문제는 오래전부터 연구되어 왔는데, 먼저 1-step TD 를 n-step TD 로 변경하여 variance 를 잡는 방법이 있다. 앞서도 설명했지만, n-step TD 는 n-step return 을 target 으로 사용한다:

\[G^{(n)}_t = R_{t+1}+\gamma R_{t+2}+...+\gamma^{n-1}R_{t+n}+\gamma^n V(S_{t+n})\]

이 방법은 A3C 나 Rainbow 에서도 사용된 방법이나, n 이라는 하이퍼파라메터가 새로이 추가된다는 문제가 있다. 이러한 문제에 대응하여 나온 방법이 여러 n-step TD 를 averaging 하여 같이 사용하는 TD(λ) 다. TD(λ) 는 각 n-step return 을 exponential moving averaging (EMA) 하여 λ-return 을 구하고, 이 때 decay factor 로 λ 가 사용된다. 여기서 하이퍼파라메터 n 대신 λ 가 추가되는데, n 에 비해 λ 가 robust 하다는 장점이 있다.

\[G^\lambda_t=(1-\lambda)\sum^\infty_{n=1}\lambda^{n-1}G^{(n)}_t\]

Advantage function 이 variance reduction 에 도움이 된다는 것은 잘 알려져 있다. GAE 에서는 이를 활용하여 λ-advantage function 을 유도한다.

\[\begin{align} &\hat A^{\text{GAE}(\gamma,\lambda)}_t = \sum^\infty_{l=0} (\gamma \lambda)^l \delta^V_{t+l} \\ &\delta^V_t=r_t+\gamma V(s_{t+1})-V(s_t) \end{align}\]

NPG

Kakade, Sham M. “A natural policy gradient.” Advances in neural information processing systems. 2002.

Natural gradients 추천 레퍼런스:

위 key idea 에 적었듯 natural policy gradient (NPG) 는 natural gradient 를 이용한 PG 다. 그러면 이 natural gradient 가 무엇이고 어떻게 이용하는지 알아봐야 할 텐데, 그 전에 먼저 그냥 gradient 에 대해서 먼저 생각해보자. Negative gradient 는 steepest descent direction 이다. 가장 경사가 가파른 방향이라는 것인데, 이게 정확히 어떤 것일까?

어떤 포인트 x 로부터 거리 $\epsilon$ 인 모든 점들의 집합 B를 생각해보자. 2차원 공간이라면 원 형태가 될 것이다. 이 $\epsilon$ 이 0으로 갈 때, 집합 B 중에서 f(x) 가 가장 작은 점으로의 방향이 steepest direction 이다. 이를 우리의 loss function L 과 parameter $\theta$ 로 대입하여 정리하면:

\[\frac{-\nabla L(\theta)}{\lVert \nabla L(\theta) \rVert} = \lim_{\epsilon \to 0} \frac{1}{\epsilon} \mathop{\text{arg min}}_{d \text{ s.t. } \lVert d \rVert = \epsilon} L(\theta + d)\]

이러한 정의는 직관적이고 전혀 문제가 없어 보이지만, 위처럼 loss function 과 $\theta$ 로 표현하면 조금 이상한 부분이 있다 - parameter 간의 distance 를 L2 distance 로 정의하는 것이 맞을까? 우리의 policy function $\pi_\theta$ 는 확률분포를 나타내는 함수다. 두 policy function 간 거리를 측정한다고 하면 이 parameter 간의 euclidean distance 가 아니라 두 확률분포간의 거리를 측정하는 것이 맞을 것이다. 따라서 natural gradient 에서는 distance 로 두 확률분포간의 divergence 를 나타내는 KL divergence 를 사용한다.

\[\frac{-\tilde\nabla L(\theta)}{\lVert \tilde\nabla L(\theta) \rVert} = \lim_{\epsilon \to 0} \frac{1}{\epsilon} \mathop{\text{arg min}}_{d \text{ s.t. } KL[\pi_\theta \Vert \pi_{\theta+d}]=\epsilon} L(\theta + d) \tag1\]

이러한 natural gradient 는 policy 의 parametrization 에 무관하게 정의하였으므로 reparametrization 에 invariant 하다는 특성을 갖는다.

One step more

조금 더 들어가보자. 위에서 natural gradient 를 정의하기는 했지만 이 값을 어떻게 구해야 할지가 문제가 된다. 먼저, KL divergence 의 local curvature Hessian 은 Fisher Information Matrix 로 나타낼 수 있다:

\[H_{KL[\pi_\theta\Vert\pi_{\theta'}]}=F\]

따라서 KL divergence 를 Taylor series 로 2차 근사하면:

\[KL[\pi_\theta\Vert\pi_{\theta+d}] \approx \frac12 d^TFd\]

그러면 여기서 최적화해야 하는 objective function $L(\theta+d)$ 도 Taylor series 로 1차 근사하여 위 (1) 식을 Lagrangian method 로 풀면 다음과 같이 constrained optimization 을 penalized optimization 으로 바꿀 수 있다:

\[\begin{align} d^* &= \mathop{\text{arg min}}_d \left[ L (\theta + d) + \lambda (KL[\pi_\theta \Vert \pi_{\theta + d}] - c) \right] \tag2 \\ &\approx \mathop{\text{arg min}}_d \left[ L(\theta) + \nabla_\theta L(\theta)^T d + \frac{1}{2} \lambda d^T F d - \lambda c \right] \end{align}\]

이 식은 d에 대한 2차함수이므로 미분하여 optimum 을 찾을 수 있다:

\[d=-\frac1\lambda F^{-1} \nabla L(\theta)\]

여기서 어차피 $\frac1\lambda$ 는 constant 이므로 learning rate 에 집어넣으면 최종적으로 natural gradient $\tilde \nabla L(\theta)$ 는:

\[\tilde \nabla L(\theta)=F^{-1}\nabla L(\theta)\]

가 된다.

TRPO

Schulman, John, et al. “Trust Region Policy Optimization.” Icml. Vol. 37. 2015.

NPG view

위에서 NPG 를 살펴보았다. TRPO 는 NPG 에서 한 걸음 더 나아간다. NPG 에서 “올바른” steepest direction 을 찾았다. 하지만 여전히 “올바른” step size 는 알 수가 없다. 어떻게 해야 할까? TRPO 에서는 backtracking line search 를 통해 이 step size 를 설정한다. Line search 란 실제로 optimization step 을 진행하기 전에 optimization direction line 위의 값들을 살펴보고 step size 를 설정하는 방법이다.

backtracking-line-search Adapted from 최적화 기법의 직관적 이해 by 다크 프로그래머

Backtracking line search 는 위 그림과 같이 먼저 이동 후 값이 좋지 않으면 되돌아오는 방법이다.

TRPO view

NPG 로부터 거쳐오면 위와 같이 설명할 수 있지만, TRPO 논문의 이론적 흐름은 사실 이렇게 흘러가지 않는다. 원래 TRPO 의 시작은 improvement guarantee 다. Key idea 에서 서술했듯, RL 에서는 한번 policy 가 망가지면 simulation 이 망가진 policy 로 되기 때문에 복구하기가 쉽지 않다.

TRPO 에서는 이 policy improvement 를 보장하기 위해, 먼저 objective function $\eta(\theta)$ 를 근사하는 $L(\theta)$ 를 찾고, 여기에 KL divergence 로 penalty 를 주었을 때 이 값이 lower bound 가 됨을 보인다.

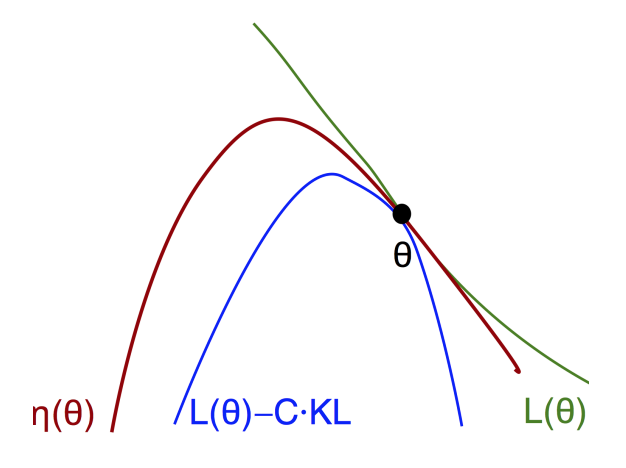
pg-trpo

이렇게 lower bound 를 찾았으니 이제 이 lower bound 를 maximize 하면 원래 objective function 도 같이 maximize 가 될 것이다. 이와 같이 lower bound 를 찾고 이를 대신 maximize 하는 방법을 Minorization-Maximization (MM) algorithm 이라고 부른다.

\[\text{maximize}_{\theta'} \left[ L_\theta(\theta') - C\cdot KL^{\max}(\theta, \theta') \right] \\ \text{where} \,\, {KL}^\text{max}(\theta,\theta')=\text{max}_{s}\left[ KL(\pi_\theta(\cdot|s) \Vert \pi_{\theta'}(\cdot|s)) \right]\]

여기서 $KL^\max$ 가 계산이 어려우므로 sampling 으로 계산이 가능하게 expectation 으로 바꾸자:

\[\text{maximize}_{\theta'} \left[ L_\theta(\theta') - C\cdot \overline{KL}_\theta(\theta, \theta') \right] \tag3 \\ \text{where} \,\, \overline{KL}_\theta(\theta,\theta')=\mathbb E_{s\sim\rho_\theta}\left[ KL(\pi_\theta(\cdot|s) \Vert \pi_{\theta'}(\cdot|s)) \right]\]

여기서 $\rho_\theta$ 는 (unnormalized) discounted state distribution 으로, 처음에 나왔던 \(d^\pi\) 의 discounted MDP 버전이다.

NPG 와 TRPO 가 유사해지는 부분이 이 부분이다. 이론적 흐름은 다르지만, NPG 에서 KL divergence constraint 를 Lagrangian method 로 penalized problem 으로 바꾸어 나오는 (2) 식이 바로 위 식에 해당한다! (따라서 위 식을 그냥 풀면 NPG 가 된다)

TRPO 에서는 NPG 와는 거꾸로 간다. Practical 하게, 이 식을 그대로 최적화하는 것 보다 hard constraint 로 변환하여 푸는 것이 large step size 를 가져갈 수 있어서 좋다고 한다:

\[\begin{align} &\text{maximize}_{\theta'} L_{\theta}(\theta') \\ &\text{subject to } \overline{KL}_\theta (\theta,\theta') \leq \delta \\ \end{align}\]

여기서 step size 를 최대한 크게 해 주기 위해서 $\overline{KL}_\theta (\theta,\theta’) = \delta$ 가 되도록 step size 를 정한다. 그리고 이게 improvement 가 보장되도록 다시 backtracking line search 를 적용하는 것이 최종 TRPO 가 된다.

한 걸음 더) Fisher information matrix (FIM) 를 직접 계산하는 것은 너무 비싼 연산이다. Conjugate gradient descent 를 이용하면 FIM 을 직접 계산하지 않고 natural gradient 를 빠르게 계산할 수 있다.

PPO

Schulman, John, et al. “Proximal policy optimization algorithms.” arXiv preprint arXiv:1707.06347 (2017).

TRPO 의 직관을 다시 정리해보자. Policy 를 업데이트 할 때 gradient 를 사용하면 step size 와 무관하게 펑펑 튈 수 있으므로 그렇지 못하도록 policy space 에 KL divergence 로 constraint 를 걸어 주어 policy 가 너무 크게 변하지 않으면서도 최대한 큰 step size 를 사용할 수 있도록 하였다. 그렇게 해서 나온 식 (3) 을 다시 쓰면:

\[\text{maximize}_{\theta'} \, \mathbb E_{\tau\sim\pi_\theta}\left[\frac{\pi_{\theta'}(a|s)}{\pi_{\theta}(a|s)}A(s,a) - C\cdot \overline{KL}_\theta(\theta, \theta') \right]\]

이다. 여기서 \(\overline{KL}_\theta\) 의 expectation (\(\mathbb E_{s\sim\rho_\theta} \left[ \cdot \right]\)) 은 바깥에도 expectation 이 있으므로 없앨 수 있고, probability ratio $r_{\theta’}(s,a)=\frac{\pi_{\theta’}(a|s)}{\pi_{\theta}(a|s)}$ 이라 하면:

\[\text{maximize}_{\theta'} \, \mathbb E_{\tau\sim\pi_\theta}\left[r_{\theta'}(s,a)A(s,a) - C\cdot KL(\theta, \theta') \right]\]

가 된다. 그런데 어차피 이걸 approximation 을 해서 풀 거라면, 그렇게 복잡하게 하지 말고 간단하게 해 보면 어떨까? PPO 에서는 두 가지 방법을 제안한다.

Clipped surrogate objective. 위에서 보면 probability ratio 함수 $r_{\theta’}(s,a)$ 가 policy 의 변화를 나타내므로, KL divergence penalty 를 쓰지 말고 그냥 이 값을 clipping 해 버리는 방법이 있다:

\[L^{CLIP}(\theta)=\mathbb E_{\tau\sim\pi_\theta} \left[ \min(r_{\theta'}(s,a)A(s,a), \text{clip}(r_{\theta'}(s,a), 1-\epsilon, 1+\epsilon)A(s,a)) \right]\]

Adaptive KL penalty coefficient. KL divergence penalty coefficient C 를 적당히 KL divergence 값을 보면서 지속적으로 조정해주는 방법도 있다:

\[L^{KLPEN}(\theta)=\mathbb E_{\tau\sim\pi_\theta}\left[r_{\theta'}(s,a)A(s,a) - \beta\cdot KL(\theta, \theta') \right]\]

이렇게 penalty coefficient 를 $\beta$ 로 두고, KL divergence 값의 변화에 따라 값이 커지면 적게 변하도록 줄여주고, 값이 작아지면 large step size 를 위해 키워주는 방식으로 조정한다.

One more important thing: multi-step optimization

기본적으로 on-policy methods 는 이론에서 현재 training policy 와 experience policy 가 동일하다고 전제하기 때문에 multi-step optimization 을 할 수 없다; 첫 번째 optimization 을 통해 training policy 가 업데이트 되면 (\(\theta \rightarrow \theta'\)) experience policy \(\theta\) 와는 달라지므로.

ppo-algorithm PPO pseudo-code

하지만 PPO 에서는 multi-step optimization 을 하는데, 사실 논문 상에서 이론적인 justification 은 없다. 처음부터 TRPO 의 다소 empirical 한 fast approximation 이 모티베이션이었던 만큼 이론적 완결성에는 크게 의미를 두지 않은 것으로 보인다. 직관적으로는 original policy 에서 크게 벗어나지 않도록 하는 penalty (or clipping) 가 들어가서 안정적인 학습이 가능해짐에 따라 multi-step optimization 을 해도 안정성을 유지할 수 있었다고 볼 수 있다.