AutoML (2) - DARTS: explanation

15 Dec 2018

Differentiable Architecture Search

Challenges

이전 글에서 gradient-based method 로 darts 를 소개했다. 그러면 gradient 기반으로 NAS 를 하려면 어떻게 해야 할까? 지금까지 gradient 를 쓰지 못했던 것은 objective function 이 non-differentiable 했기 때문이었다. 그렇다면 이걸 어떻게 해야 differentiable 하게 만들 수 있을까?

가장 먼저 objective function 을 validaton accuracy 에서 validation loss 로 바꾸자. Accuracy 는 measure 자체가 non-differentiable 이므로 적합하지 않다. 그러면 validation loss 에 대해 controller parameters 가 미분 가능하면 된다. 당연한 얘기지만 우리가 만드는 child network 는 미분 가능하다. 그럼 뭐가 문제인가? controller 가 child network 를 만들어내는 과정이 문제인 것이다. RNN controller 를 사용하는 RL 기반 방법론들을 생각해보자. RNN 이 네트워크의 구조를 하나씩 생성한다. 이대로 child network 가 만들어지고 학습된다. 이 RNN output 이 child network 가 되는 과정이 non-differentiable 하기 때문에 gradient 기반 학습이 불가능하다.

Continuous relaxation

ResNet 같은 skip-connection 도, Inception 같은 브랜치도 없는 VGG 같은 시퀀셜한 구조를 생각해보자. 이 제약조건 아래에서 NAS 를 한다고 하면 어떨까? TNAS 나 ENAS 에서 도입한 topology 도 필요 없고, NAS 논문에서 처음에 했던 것처럼 어떤 연산을 할 것인지만 결정해서 시퀀셜하게 쭉 이으면 된다. 이 연산을 결정하는 것이 RNN controller 이며, RNN 이 각 레이어마다 하나씩 연산의 종류를 뱉어낸다. RNN 은 각 연산들에 대해서 softmax 를 통해 각각 확률값을 뱉을 것이고, 이 중 최대값이 child network 의 연산이 된다. 문제는 바로 이 부분인데, max 를 통해 최대값을 고르고 그 연산으로 child network 를 만드는 작업이 non-differentiable 한 것이다.

해결책은 사실 간단하다. max 를 취하지 말고 softmax 값을 그대로 쓰면 된다. Softmax 값을 그대로 쓰기 위해서 이 논문에서는 레이어에 연산의 종류를 하나로 정하는 것이 아니라 모든 연산을 다 사용하고 이 softmax 값을 각 연산의 가중치로 사용한다. 각 레이어는 모든 연산을 다 가지고 있으므로 각 레이어의 연산을 mixed operation 이라 한다.

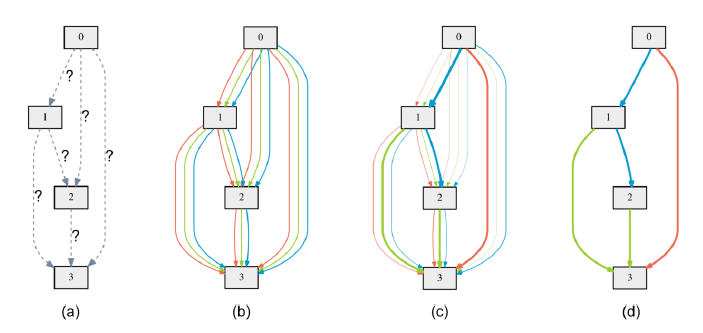
상상하기 쉽도록 topology 를 없앴지만 당연히 있는것이 좋다. DARTS 에서도 ENAS 와 같은 DAG topology 를 차용한다. 단 여기서는 노드의 색이 연산의 종류가 아니라 엣지의 색이 연산의 종류다. (b) 를 보면 모든 엣지들이 3개씩 존재하는데, 3종류의 연산이 전부 다 살아 있는 것이다. (c) 학습이 진행되면 가중치가 학습되면서 일부 연산만이 살아남게 된다. (d) 는 최종적으로 높은 가중치를 가진 연산들만을 남긴 것이다.

Removing RNN

RL 기반 방법론에서 RNN 의 역할은 현재 스테이트를 기반으로 다음 액션을 결정하는 것이다. 즉, 지금까지 만든 네트워크 구조를 기반으로 나머지 부분을 어떻게 만들어야 더 좋은 네트워크가 나올지를 고민하고 결정하는 역할인 것이다. 이 고민이 필요한 이유는 RL 기반 방법론에서는 액션에 대한 피드백이 점수로만 오지 구체적으로 어떤 부분을 어떻게 개선해야 할지를 알려주지 않기 때문이다. 하지만 gradient-based method 에서는 이 부분에 대한 정보가 gradient 를 통해서 넘어오기 때문에 RNN 이 필요하지 않다. 즉, 각 연산들의 가중치 값이 파라메터가 되고 이게 곧 컨트롤러인 것이다!

Optimization

일반적으로 NAS 에서는 데이터셋을 3종류로 나눈다. child network 를 학습시킬 training 데이터셋, 그 네트워크의 성능을 확인할 validation 데이터셋, 그리고 최종적으로 찾은 구조의 성능을 테스트할 test 데이터셋.

$\alpha$ 를 각 연산들에 대한 가중치 파라메터라 하고, $w$ 를 모든 연산들의 weights 라 하자. 그러면 우리가 최종적으로 minimize 하고 싶은 값은 validation loss $L_{val}(w^*,\alpha)$ 이 된다. 즉, validation loss 가 최소가 되도록 $\alpha$ 를 최적화하고 싶은데 이 때 validation loss 를 계산하기 위한 가중치값 $w$ 는 트레이닝 데이터셋에 대해 최적화가 되어 있어야 한다. 이를 식으로 나타내면 다음과 같다:

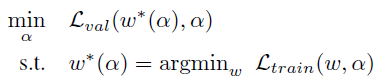
GAN 을 아는 사람이라면 이 부분이 GAN 과 유사하다는 것을 느꼈을 것이다. 실제로 학습 시에도 GAN 처럼 $w$ 와 $\alpha$ 를 1 step 씩 번갈아가며 학습한다. $w^*$ 를 매번 구하는 것이 너무 많은 리소스를 필요로 하기 때문에 approximation 을 하는 것이다.

Algorithm

지금까지 설명한 것을 코드로 표현하면 위와 같다. 먼저 $\alpha$ 를 가중치 파라메터로 갖는 mixed operation 을 생성한다. 이 mixed operation 은 모든 후보 연산들의 weighted sum 이며, 이 연산들의 weights 가 $w$ 에 해당한다.

이제 GAN 처럼 1-step 씩 학습을 수행한다. Training 데이터셋에 대해 $w$ 를 먼저 최적화하고, validation 데이터셋에 대해 $\alpha$ 를 학습한다. 이 과정을 수렴할때까지 반복한 후, 마지막으로 가중치가 높은 파라메터들을 골라 실제 구조를 정한다.

그런데 잘 보면 $L_{val}$ 을 최적화하는 식이 좀 이상하다. 이는 approximation 을 조금 더 정확하게 하기 위해 gradient unrolling 을 하기 때문이다. $\alpha$ 의 그라디언트를 계산할 때 바로 하는 것이 아니라, 1-step 더 가상으로 이동시킨 child network weight $w$ 를 계산한다. 원래대로라면 optimal $w^*$ 에 대해 계산해야 하는 것이기 때문에 조금이라도 그에 가깝게 만들어주기 위해서 1-step 을 가상으로 이동시킨다.

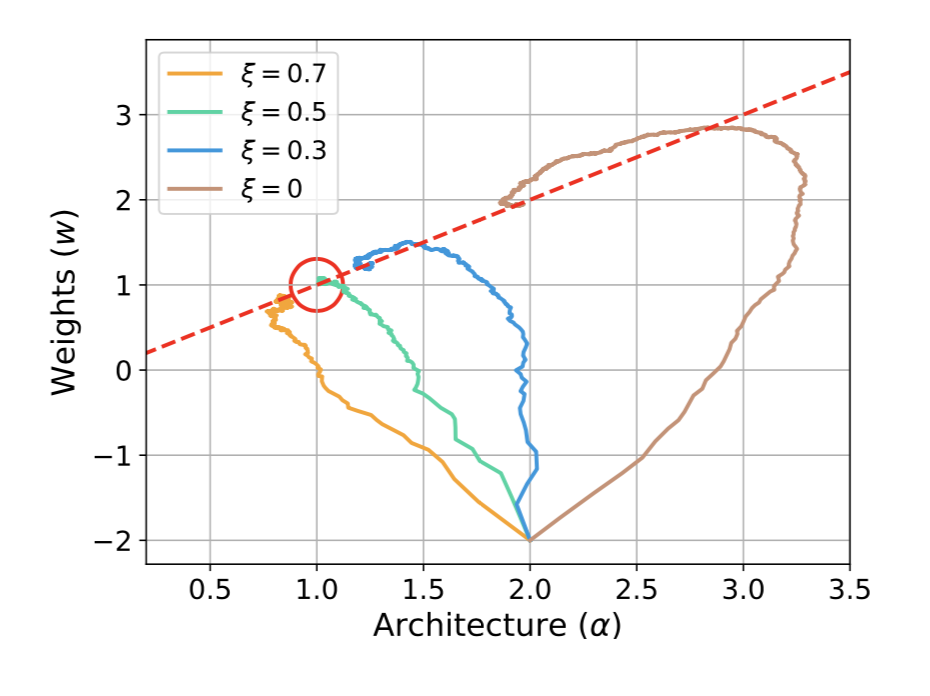
위 그래프에서 이러한 virtual step 을 사용했을 때와 사용하지 않았을 때의 수렴성 차이를 확인할 수 있다. 빨간색 점선은 주어진 $\alpha$ 에 대해 $w$ 가 최적화 되었을 때의 라인으로 local optima 에 해당하고, 좌표 (1, 1) 의 빨간색 원은 global optima 에 해당한다. Virtual step 을 사용하지 않으면 수렴 속도도 느려질 뿐더러 global optima 에서 먼 local optima 로 수렴하는 것을 확인할 수 있다.

Results

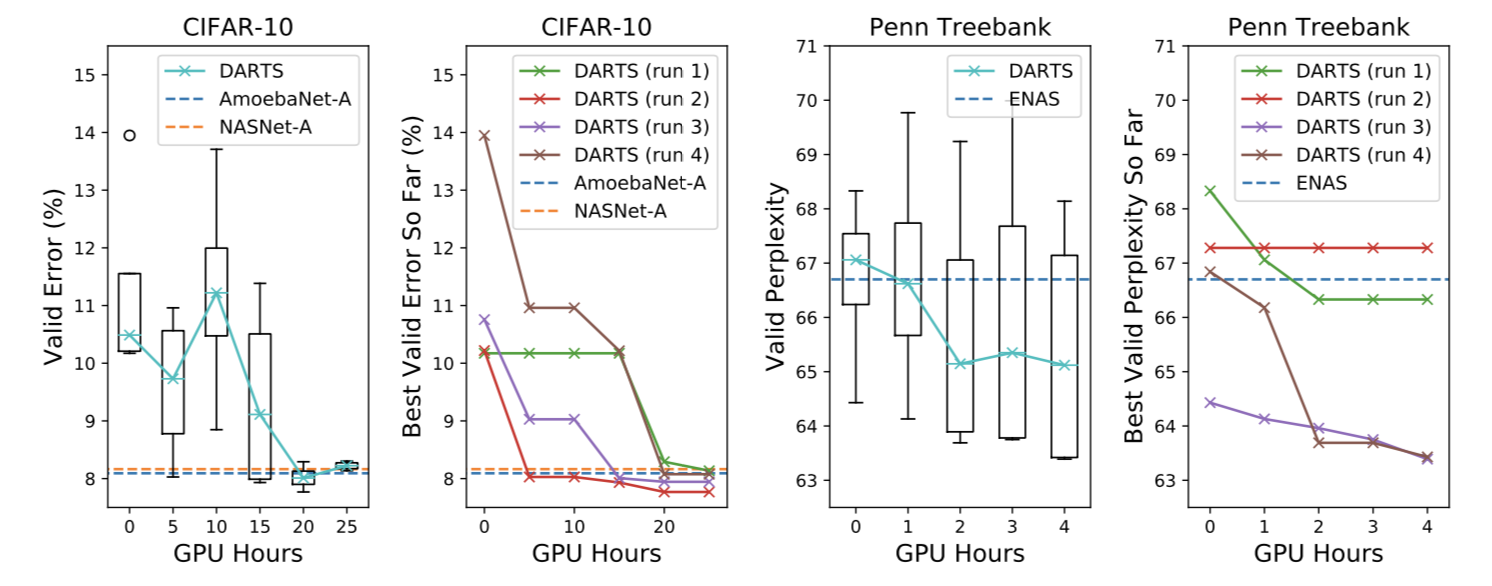
CIFAR10 에 대한 CNN cell 탐색 및 Penn Treebank 에 대한 RNN cell 탐색 그래프.

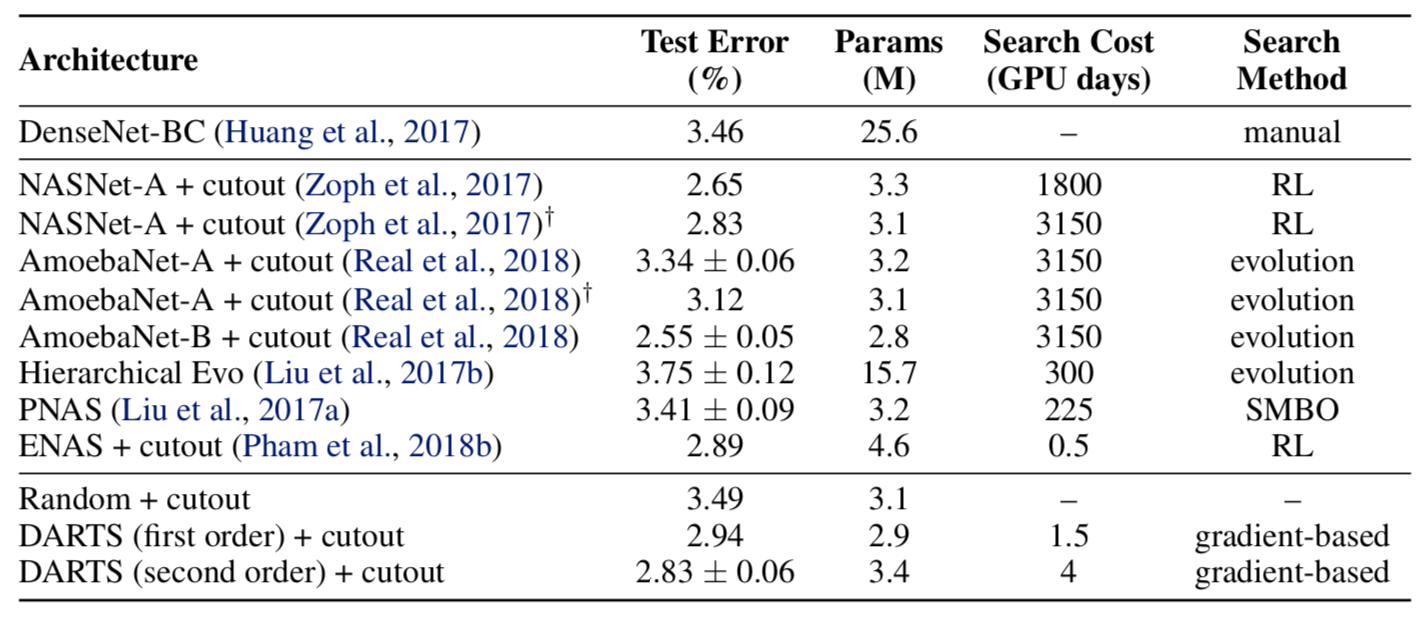
CIFAR10 에 대한 성능 비교표. Second-order 가 앞서 설명한 gradient unrolling 을 적용한 버전이다. 다른 알고리즘들과 비교해서 충분히 강력한 성능 (test error) 과, 매우 적은 search cost 를 확인할 수 있다.

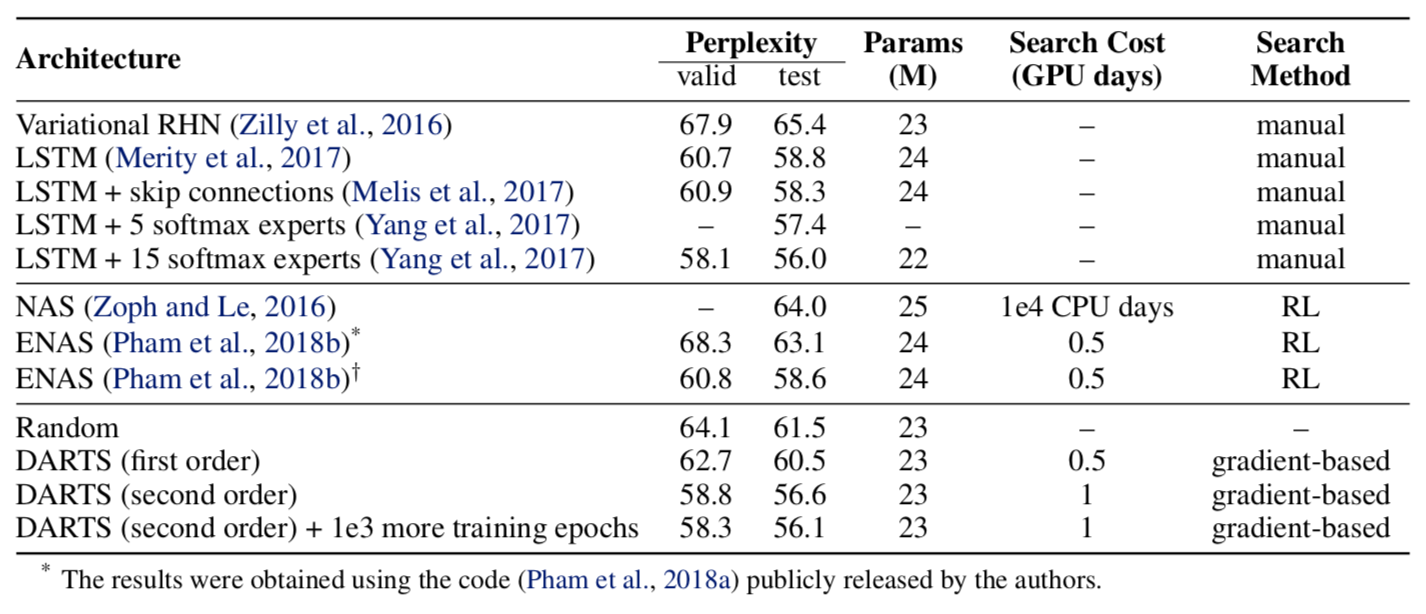
Penn Treebank 에 대한 language model 성능 비교표. SOTA 를 갱신하지는 못했지만 그에 준하는 성능을 보였으며, NAS 중에서는 가장 좋은 성능을 보였다.

Conclusion

DARTS 는 최초의 differentiable NAS 알고리즘으로, 다른 non-differentiable NAS 방법들과 비교하여 test error 와 search cost 측면에서 강력한 성능을 보였다. 개인적으로 NAS 논문 중에서 가장 인상적으로 읽었으며, 앞으로도 더 발전할 여지가 많다고 생각하여 여러모로 기대하고 있다.